Note
Go to the end to download the full example code.
Modeling Cavitation#
This example examines the pressure-driven cavitating flow of water through a sharp-edged orifice. This is a typical configuration in fuel injectors, and brings a challenge to the physics and numerics of cavitation models because of the high pressure differentials involved and the high ratio of liquid to vapor density.
This example uses the multiphase modeling capability of Ansys Fluent, and will be able to predict the strong cavitation near the orifice after flow separation at a sharp edge.
Workflow tasks
This example demonstrates how to do the following:
Set boundary conditions for internal flow
Use the mixture model with cavitation effects
Calculate a solution using the pressure-based coupled solver
Problem description
The problem considers the cavitation caused by the flow separation after a sharp-edged orifice. The flow is pressure driven, with an inlet pressure of 500 kPa and an outlet pressure of 95 kPa. The orifice diameter is 4 mm, and the geometrical parameters of the orifice are D/d = 2.88 and L/d = 4, where D, d, and L are the inlet diameter, orifice diameter, and orifice length respectively.
Example Setup#
Before you can begin, you must set up the example and initialize this workflow.
Launch Fluent#
Perform required imports, which includes downloading and importing the geometry file.
import ansys.fluent.core as pyfluent
from ansys.fluent.core import examples
cav_file = examples.download_file("cav.msh.gz", "pyfluent/cavitation")
Launch a Fluent session in the 2d solution mode with double precision running on four processors and print Fluent version.
solver = pyfluent.launch_fluent(
precision="double",
processor_count=4,
mode="solver",
version="2d",
)
print(solver.get_fluent_version())
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/utils/deprecate.py:49: PyFluentDeprecationWarning: 'version' is deprecated. Use 'dimension' instead.
return func(*args, **kwargs)
Fluent version 2025 R1
Read the mesh that was downloaded.
solver.file.read_mesh(file_name=cav_file)
solver.mesh.check()
Reading "\"| gunzip -c \\\"cav.msh.gz\\\"\""...
Buffering for file scan...
3716 nodes.
170 mixed wall faces, zone 3.
20 mixed pressure-outlet faces, zone 4.
120 mixed axis faces, zone 5.
25 mixed axis faces, zone 6.
25 mixed pressure-inlet faces, zone 7.
20 mixed pressure-inlet faces, zone 8.
6860 mixed interior faces, zone 10.
3525 quadrilateral cells, zone 2.
Building...
mesh
auto partitioning mesh by Metis (fast),
distributing mesh
parts....,
faces....,
nodes....,
cells....,
bandwidth reduction using Reverse Cuthill-McKee: 625/25 = 25
materials,
interface,
domains,
zones,
default-interior
inlet_1
inlet_2
symm_1
symm_2
outlet
wall
fluid
parallel,
Done.
Warning: The use of axis boundary conditions is not appropriate for
a 2D/3D flow problem. Please consider changing the zone
type to symmetry or wall, or the problem to axisymmetric.
Warning: The use of axis boundary conditions is not appropriate for
a 2D/3D flow problem. Please consider changing the zone
type to symmetry or wall, or the problem to axisymmetric.
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'mesh' is deprecated. Use 'settings.mesh' instead.
warnings.warn(
Domain Extents:
x-coordinate: min (m) = -1.600000e-02, max (m) = 3.200000e-02
y-coordinate: min (m) = 0.000000e+00, max (m) = 1.152000e-02
Volume statistics:
minimum volume (m3): 5.333266e-08
maximum volume (m3): 4.445774e-07
total volume (m3): 3.123200e-04
Face area statistics:
minimum face area (m2): 1.999997e-04
maximum face area (m2): 1.107099e-03
Checking mesh.....................................
Done.
Specify an axisymmetric model.
solver.setup.general.solver.two_dim_space = "axisymmetric"
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'setup' is deprecated. Use 'settings.setup' instead.
warnings.warn(
Enable the multiphase mixture model.
solver.setup.models.multiphase.models = "mixture"
solver.tui.define.models.multiphase.mixture_parameters("no", "implicit")
Changing Discretization Scheme for Momentum to First Order Upwind
Pseudo Time Method settings are adjusted.
Adjusting the following settings:
Changing Discretization Scheme for Turbulent Kinetic Energy: from: Second Order Upwind to: First Order Upwind
Changing Discretization Scheme for Specific Dissipation Rate: from: Second Order Upwind to: First Order Upwind
Changing Discretization Scheme for Pressure to PRESTO!
Enable the k-ω SST turbulence model.
solver.setup.models.viscous = {
"model": "k-omega",
"k_omega_model": "sst",
}
Define materials#
Create a material named water, using 1000 kg/m3 for density and 0.001 kg/m–s for viscosity. Then, copy water vapor properties from the database and modify the copy by changing the density to 0.02558 kg/m3 and the viscosity to 1.26e-06 kg/m–s.
solver.setup.materials.fluid["water"] = {
"density": {
"option": "constant",
"value": 1000,
},
"viscosity": {
"option": "constant",
"value": 0.001,
},
}
solver.setup.materials.database.copy_by_name(type="fluid", name="water-vapor")
solver.setup.materials.fluid["water-vapor"] = {
"density": {"value": 0.02558},
"viscosity": {"value": 1.26e-06},
}
Material "water-vapor" copied from database: fluent-database.
Phases#
Change the name of the primary phase to “liquid” and the secondary phase to “water-vapor”. Then, enable the cavitation model and set the number of mass transfer mechanisms to 1. Finally, specify cavitation as a mass transfer mechanism occurring from the liquid to the vapor.
solver.tui.define.phases.set_domain_properties.change_phases_names("vapor", "liquid")
solver.tui.define.phases.set_domain_properties.phase_domains.liquid.material(
"yes", "water"
)
solver.tui.define.phases.set_domain_properties.phase_domains.vapor.material(
"yes", "water-vapor"
)
solver.tui.define.phases.set_domain_properties.interaction_domain.heat_mass_reactions.mass_transfer(
1, "liquid", "vapor", "cavitation", "1", "no", "no", "no"
)
Warning: For user-defined mass transfer, Linearized-Mass-Transfer UDF is on. If needed, use 'solve/set/expert' to switch to Mass-Transfer UDF.
Mass Transfer
Boundary Conditions#
For the first inlet momentum boundary conditions set the direction specification method to ‘normal to boundary’, gauge total pressure as 500 kPa and supersonic or initial gauge pressure as 449 kPa.
For the turbulence settings choose ‘Intensity and Viscosity Ratio’ for turbulent specification. Set turbulent intensity and turbulent viscosity ratio to 0.05 and 10 respectively.
inlet_1 = solver.setup.boundary_conditions.pressure_inlet["inlet_1"].phase
inlet_1["mixture"] = {
"momentum": {
"gauge_total_pressure": {"value": 500000},
"supersonic_or_initial_gauge_pressure": {"value": 449000},
"direction_specification_method": "Normal to Boundary",
},
"turbulence": {
"turbulent_specification": "Intensity and Viscosity Ratio",
"turbulent_intensity": 0.05,
"turbulent_viscosity_ratio": 10,
},
}
Before copying inlet_1’s boundary conditions to inlet_2, set the vapor fraction to 0.
inlet_1["vapor"] = {
"multiphase": {
"volume_fraction": {"value": 0},
},
}
solver.setup.boundary_conditions.copy(from_="inlet_1", to="inlet_2")
Copy inlet_1 boundary conditions to inlet_2
For the outlet boundary conditions, set the gauge pressure as 95 kPa. Use the same turbulence and volume fraction settings as the inlets.
outlet = solver.setup.boundary_conditions.pressure_outlet["outlet"].phase
outlet["mixture"] = {
"momentum": {
"gauge_pressure": {"value": 95000},
},
"turbulence": {
"turbulent_specification": "Intensity and Viscosity Ratio",
"turbulent_intensity": 0.04,
"turbulent_viscosity_ratio": 10,
},
}
outlet["vapor"] = {
"multiphase": {
"volume_fraction": {"value": 0},
},
}
Operating Conditions#
Set the operating pressure to 0.
solver.setup.general.operating_conditions.operating_pressure = 0
Solution#
To configure the discretization scheme, set ‘first order upwind’ method for turbulent kinetic energy and turbulent dissipation rate, ‘quick’ for the momentum and volume fraction, and ‘presto!’ for pressure.
methods = solver.solution.methods
methods.discretization_scheme = {
"k": "first-order-upwind",
"mom": "quick",
"mp": "quick",
"omega": "first-order-upwind",
"pressure": "presto!",
}
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'solution' is deprecated. Use 'settings.solution' instead.
warnings.warn(
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/solver/flobject.py:637: DeprecatedSettingWarning: Note: A newer syntax is available to perform the last operation:
solver.settings.solution.methods.spatial_discretization.discretization_scheme = {"pressure" : "presto!", "k" : "first-order-upwind", "omega" : "first-order-upwind", "mom" : "quick", "mp" : "quick"}
warnings.warn(
For the pressure velocity coupling scheme choose ‘Coupled’. Set the pseudo time step method to ‘global time step’ and enable ‘High Order Term Relaxation’. Then, set the explicit relaxation factor for ‘Volume Fraction’ to 0.3.
methods.p_v_coupling.flow_scheme = "Coupled"
methods.pseudo_time_method.formulation.coupled_solver = "global-time-step"
methods.high_order_term_relaxation.enable = True
solver.solution.controls.pseudo_time_explicit_relaxation_factor.global_dt_pseudo_relax[
"mp"
] = 0.3
To plot the residuals, enable plotting and set the convergence criteria to 1e-05 for x-velocity, y-velocity, k, omega, and vf-vapor. Enable the specified initial pressure then initialize the solution with hybrid initialization.
resid_eqns = solver.solution.monitor.residual.equations
resid_eqns["continuity"].absolute_criteria = 1e-5
resid_eqns["x-velocity"].absolute_criteria = 1e-5
resid_eqns["y-velocity"].absolute_criteria = 1e-5
resid_eqns["k"].absolute_criteria = 1e-5
resid_eqns["omega"].absolute_criteria = 1e-5
resid_eqns["vf-vapor"].absolute_criteria = 1e-5
initialization = solver.solution.initialization
initialization.initialization_type = "hybrid"
initialization.hybrid_init_options.general_settings.initial_pressure = True
initialization.hybrid_initialize()
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/solver/flobject.py:637: DeprecatedSettingWarning: Note: A newer syntax is available to perform the last operation:
solver.settings.solution.initialization.hybrid_init_options.general_settings.initialization_options.initial_pressure = True
warnings.warn(
Initialize using the hybrid initialization method.
Checking case topology...
-This case has both inlets & outlets
-Pressure information is available at the boundaries
iter scalar-0 scalar-1
1 1.000000e+00 1.000000e+00
2 1.296584e-06 1.125210e-05
3 1.235818e-07 1.051320e-06
4 7.465480e-09 7.605226e-08
5 6.628479e-10 5.081937e-09
6 4.004979e-11 3.953780e-10
7 2.030450e-12 3.202392e-11
8 7.102260e-14 2.627088e-12
9 2.330916e-14 2.165282e-13
10 7.959646e-15 1.787909e-14
Hybrid initialization is done.
Save and Run#
Save the case file ‘cav.cas.h5’. Then, start the calculation by requesting 500 iterations. Save the final case file and the data.
solver.file.write_case(file_name="cav.cas.h5")
solver.solution.run_calculation.iterate(iter_count=500)
solver.file.write_case_data(file_name="cav.cas.h5")
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'file' is deprecated. Use 'settings.file' instead.
warnings.warn(
Fast-loading "/ansys_inc/v251/fluent/fluent25.1.0/addons/afd/lib/hdfio.bin"
Done.
Writing to a16bfeaf8838:"/mnt/pyfluent/cav.cas.h5" in NODE0 mode and compression level 1 ...
Grouping cells for Laplace smoothing ...
3525 cells, 1 zone ...
7240 faces, 7 zones ...
3716 nodes, 1 zone ...
Done.
Done.
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'solution' is deprecated. Use 'settings.solution' instead.
warnings.warn(
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
1 1.0000e+00 2.2228e-03 1.8821e-03 9.6702e-01 4.9103e-01 0.0000e+00 0:00:35 499
2 7.3292e-01 1.6532e-03 1.0743e-03 8.5319e-01 4.8715e-01 1.1939e-05 0:00:39 498
3 1.0000e+00 1.6151e-03 6.7638e-04 2.5886e-01 4.8014e-01 1.7993e+01 0:00:38 497
4 1.0000e+00 1.8743e-03 5.4489e-04 4.7126e-02 4.7219e-01 2.2482e+00 0:00:37 496
5 1.0000e+00 2.4997e-03 6.3771e-04 1.6582e-02 4.6205e-01 8.6573e-01 0:00:37 495
6 9.0777e-01 2.7827e-03 7.0239e-04 2.0840e-02 4.4841e-01 4.6992e-01 0:00:36 494
7 7.3084e-01 2.9148e-03 7.8166e-04 2.6382e-02 4.3051e-01 2.8999e-01 0:00:36 493
8 5.5966e-01 3.1875e-03 7.7544e-04 3.1756e-02 4.0816e-01 1.8951e-01 0:00:35 492
9 4.1711e-01 3.4774e-03 1.1262e-03 3.5216e-02 3.8009e-01 1.3313e-01 0:00:35 491
10 3.0686e-01 3.6791e-03 9.2507e-04 3.7677e-02 3.5017e-01 9.5494e-02 0:00:34 490
11 2.2207e-01 3.7418e-03 1.0029e-03 4.1539e-02 3.1459e-01 7.1571e-02 0:00:34 489
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
12 1.6365e-01 3.9077e-03 9.7971e-04 4.3597e-02 2.7930e-01 5.5726e-02 0:00:35 488
13 1.2126e-01 4.0000e-03 1.0536e-03 4.5916e-02 2.4520e-01 4.4709e-02 0:00:35 487
14 8.9805e-02 3.9648e-03 1.1459e-03 4.7526e-02 2.1282e-01 3.7114e-02 0:00:34 486
15 6.6406e-02 3.8723e-03 1.1330e-03 5.0287e-02 1.8385e-01 3.1794e-02 0:00:34 485
16 4.9353e-02 3.8678e-03 1.1420e-03 5.1879e-02 1.5703e-01 2.7665e-02 0:00:34 484
17 3.8251e-02 3.6707e-03 1.1166e-03 5.1282e-02 1.3301e-01 2.4531e-02 0:00:34 483
18 3.0818e-02 3.3954e-03 1.0492e-03 5.1487e-02 1.1186e-01 2.2381e-02 0:00:33 482
19 2.5629e-02 3.1671e-03 1.0293e-03 5.3981e-02 9.4319e-02 2.0938e-02 0:00:33 481
Reversed flow on 1 face of pressure-outlet 4.
20 2.1476e-02 3.0261e-03 9.6715e-04 7.6034e-02 7.9693e-02 2.0704e-02 0:00:33 480
Reversed flow on 2 faces of pressure-outlet 4.
21 1.7943e-02 2.8269e-03 9.1671e-04 8.0161e-02 6.7287e-02 2.0893e-02 0:00:33 479
Reversed flow on 3 faces of pressure-outlet 4.
22 1.6035e-02 2.7010e-03 8.8850e-04 7.1001e-02 5.7998e-02 2.1426e-02 0:00:34 478
Reversed flow on 4 faces of pressure-outlet 4.
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
23 1.4228e-02 2.5902e-03 8.1509e-04 6.8013e-02 5.0146e-02 2.3732e-02 0:00:35 477
Reversed flow on 13 faces of pressure-outlet 4.
24 1.2587e-02 2.5387e-03 7.6853e-04 6.4659e-02 4.5312e-02 2.5396e-02 0:00:34 476
Reversed flow on 15 faces of pressure-outlet 4.
25 1.1796e-02 2.3170e-03 6.5794e-04 6.0139e-02 3.8480e-02 2.6522e-02 0:00:34 475
Reversed flow on 16 faces of pressure-outlet 4.
26 1.1683e-02 2.0643e-03 5.4545e-04 5.6012e-02 3.3267e-02 2.7460e-02 0:00:34 474
Reversed flow on 16 faces of pressure-outlet 4.
27 1.0857e-02 1.8765e-03 4.6771e-04 5.0303e-02 2.9457e-02 2.7975e-02 0:00:34 473
Reversed flow on 16 faces of pressure-outlet 4.
28 9.8971e-03 1.7366e-03 4.1276e-04 4.3135e-02 2.6321e-02 2.7906e-02 0:00:35 472
Reversed flow on 15 faces of pressure-outlet 4.
29 8.8656e-03 1.5824e-03 3.5971e-04 3.5937e-02 2.3646e-02 2.7212e-02 0:00:34 471
Reversed flow on 15 faces of pressure-outlet 4.
30 7.8407e-03 1.4410e-03 3.1553e-04 3.0797e-02 2.1404e-02 2.5966e-02 0:00:34 470
Reversed flow on 14 faces of pressure-outlet 4.
31 6.9191e-03 1.2912e-03 2.8204e-04 2.8064e-02 1.9013e-02 2.4392e-02 0:00:34 469
Reversed flow on 14 faces of pressure-outlet 4.
32 6.2367e-03 1.1585e-03 2.5730e-04 2.5136e-02 1.6447e-02 2.2803e-02 0:00:33 468
Reversed flow on 13 faces of pressure-outlet 4.
33 5.7563e-03 1.0447e-03 2.3278e-04 2.4102e-02 1.4331e-02 2.1336e-02 0:00:33 467
Reversed flow on 13 faces of pressure-outlet 4.
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
34 5.3357e-03 9.4182e-04 2.1562e-04 2.3503e-02 1.3050e-02 2.0002e-02 0:00:32 466
Reversed flow on 12 faces of pressure-outlet 4.
35 4.9474e-03 8.5706e-04 1.9868e-04 2.2794e-02 1.1909e-02 1.8855e-02 0:00:32 465
Reversed flow on 12 faces of pressure-outlet 4.
36 4.5944e-03 7.8655e-04 1.8811e-04 2.2522e-02 1.1602e-02 1.7847e-02 0:00:32 464
Reversed flow on 11 faces of pressure-outlet 4.
37 4.2778e-03 7.2887e-04 1.7466e-04 2.0923e-02 1.1233e-02 1.7055e-02 0:00:32 463
Reversed flow on 10 faces of pressure-outlet 4.
38 4.0397e-03 6.8505e-04 1.6895e-04 2.0783e-02 1.0709e-02 1.6487e-02 0:00:32 462
Reversed flow on 9 faces of pressure-outlet 4.
39 3.8684e-03 6.3769e-04 1.6022e-04 1.9463e-02 1.0462e-02 1.6059e-02 0:00:32 461
Reversed flow on 9 faces of pressure-outlet 4.
40 3.6540e-03 5.7872e-04 1.5160e-04 1.7005e-02 9.9463e-03 1.5704e-02 0:00:32 460
Reversed flow on 8 faces of pressure-outlet 4.
41 3.3797e-03 5.1907e-04 1.3934e-04 1.4983e-02 8.9500e-03 1.5354e-02 0:00:32 459
Reversed flow on 8 faces of pressure-outlet 4.
42 3.1636e-03 4.5909e-04 1.2609e-04 1.3126e-02 8.3316e-03 1.5009e-02 0:00:32 458
Reversed flow on 7 faces of pressure-outlet 4.
43 2.8819e-03 4.0810e-04 1.1567e-04 1.1612e-02 7.4048e-03 1.4658e-02 0:00:32 457
Reversed flow on 7 faces of pressure-outlet 4.
44 2.6622e-03 3.5845e-04 1.0255e-04 1.0465e-02 6.8731e-03 1.4337e-02 0:00:32 456
Reversed flow on 7 faces of pressure-outlet 4.
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
45 2.4051e-03 3.1858e-04 9.2025e-05 9.3658e-03 6.3750e-03 1.4069e-02 0:00:32 455
Reversed flow on 7 faces of pressure-outlet 4.
46 2.2816e-03 2.8383e-04 8.2625e-05 8.5871e-03 6.0424e-03 1.3856e-02 0:00:32 454
Reversed flow on 6 faces of pressure-outlet 4.
47 2.1403e-03 2.5411e-04 7.4956e-05 7.6707e-03 5.9147e-03 1.3674e-02 0:00:32 453
Reversed flow on 6 faces of pressure-outlet 4.
48 2.0730e-03 2.2961e-04 6.6434e-05 7.2136e-03 5.4542e-03 1.3504e-02 0:00:32 452
Reversed flow on 6 faces of pressure-outlet 4.
49 2.0003e-03 2.0799e-04 6.1948e-05 6.7506e-03 5.1981e-03 1.3354e-02 0:00:31 451
Reversed flow on 6 faces of pressure-outlet 4.
50 1.9294e-03 1.9086e-04 5.7112e-05 6.2716e-03 4.9583e-03 1.3226e-02 0:00:32 450
Reversed flow on 6 faces of pressure-outlet 4.
51 1.8944e-03 1.7650e-04 5.2941e-05 5.8021e-03 4.7563e-03 1.3107e-02 0:00:31 449
Reversed flow on 6 faces of pressure-outlet 4.
52 1.8623e-03 1.6515e-04 4.9972e-05 5.5410e-03 4.5788e-03 1.2974e-02 0:00:32 448
Reversed flow on 6 faces of pressure-outlet 4.
53 1.8225e-03 1.5604e-04 4.7795e-05 5.3216e-03 4.3962e-03 1.2836e-02 0:00:32 447
Reversed flow on 6 faces of pressure-outlet 4.
54 1.7982e-03 1.4914e-04 4.5926e-05 5.0760e-03 4.2480e-03 1.2689e-02 0:00:31 446
Reversed flow on 6 faces of pressure-outlet 4.
55 1.7742e-03 1.4304e-04 4.5047e-05 4.8550e-03 3.9638e-03 1.2516e-02 0:00:31 445
Reversed flow on 5 faces of pressure-outlet 4.
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
56 1.7504e-03 1.4048e-04 4.5753e-05 4.7744e-03 4.0246e-03 1.2315e-02 0:00:31 444
Reversed flow on 5 faces of pressure-outlet 4.
57 1.7275e-03 1.3844e-04 4.6048e-05 4.9266e-03 3.6754e-03 1.2071e-02 0:00:30 443
Reversed flow on 5 faces of pressure-outlet 4.
58 1.6936e-03 1.3439e-04 4.5747e-05 4.7639e-03 3.4596e-03 1.1798e-02 0:00:31 442
Reversed flow on 5 faces of pressure-outlet 4.
59 1.6732e-03 1.3154e-04 4.5732e-05 4.5742e-03 3.2553e-03 1.1500e-02 0:00:30 441
Reversed flow on 5 faces of pressure-outlet 4.
60 1.6424e-03 1.3050e-04 4.3914e-05 4.4956e-03 3.1049e-03 1.1178e-02 0:00:30 440
Reversed flow on 5 faces of pressure-outlet 4.
61 1.5982e-03 1.3165e-04 4.3657e-05 4.3805e-03 2.9765e-03 1.0829e-02 0:00:30 439
Reversed flow on 4 faces of pressure-outlet 4.
62 1.5431e-03 1.3509e-04 4.5286e-05 4.7304e-03 3.1080e-03 1.0442e-02 0:00:30 438
Reversed flow on 4 faces of pressure-outlet 4.
63 1.5021e-03 1.3958e-04 4.5200e-05 5.2678e-03 3.0131e-03 1.0006e-02 0:00:30 437
Reversed flow on 4 faces of pressure-outlet 4.
64 1.4398e-03 1.4129e-04 4.4941e-05 5.3808e-03 2.9819e-03 9.5258e-03 0:00:30 436
Reversed flow on 3 faces of pressure-outlet 4.
65 1.3742e-03 1.4269e-04 4.4583e-05 5.6070e-03 3.0231e-03 9.0061e-03 0:00:30 435
Reversed flow on 3 faces of pressure-outlet 4.
66 1.3071e-03 1.4346e-04 4.2556e-05 5.8217e-03 2.9304e-03 8.4458e-03 0:00:30 434
Reversed flow on 3 faces of pressure-outlet 4.
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
67 1.2129e-03 1.4258e-04 3.9724e-05 5.8671e-03 2.8767e-03 7.8561e-03 0:00:29 433
Reversed flow on 2 faces of pressure-outlet 4.
68 1.1227e-03 1.4144e-04 3.7832e-05 5.9340e-03 2.8566e-03 7.2496e-03 0:00:30 432
Reversed flow on 2 faces of pressure-outlet 4.
69 1.0334e-03 1.3955e-04 3.4890e-05 6.1431e-03 2.6506e-03 6.6300e-03 0:00:30 431
Reversed flow on 1 face of pressure-outlet 4.
70 9.2583e-04 1.3696e-04 3.2659e-05 6.1994e-03 2.5946e-03 6.0107e-03 0:00:30 430
Reversed flow on 1 face of pressure-outlet 4.
71 8.3662e-04 1.3188e-04 3.0132e-05 6.1475e-03 2.5067e-03 5.4038e-03 0:00:30 429
72 7.4160e-04 1.2523e-04 2.7516e-05 5.9937e-03 2.4219e-03 4.8274e-03 0:00:30 428
73 6.6008e-04 1.1785e-04 2.5294e-05 5.7681e-03 2.3189e-03 4.2823e-03 0:00:29 427
74 5.9196e-04 1.0984e-04 2.4009e-05 5.4754e-03 2.1873e-03 3.7831e-03 0:00:29 426
75 5.5061e-04 1.0170e-04 2.2885e-05 5.1641e-03 2.0401e-03 3.3371e-03 0:00:30 425
76 5.1703e-04 9.4135e-05 2.2019e-05 4.8131e-03 1.8867e-03 2.9469e-03 0:00:30 424
77 4.9405e-04 8.7131e-05 2.1437e-05 4.4270e-03 1.7409e-03 2.6882e-03 0:00:30 423
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
78 4.7088e-04 8.0800e-05 2.1057e-05 4.0525e-03 1.6111e-03 2.4984e-03 0:00:30 422
79 4.4791e-04 7.5122e-05 2.0072e-05 3.6867e-03 1.4901e-03 2.3503e-03 0:00:30 421
80 4.2778e-04 6.9804e-05 1.8560e-05 3.3191e-03 1.3720e-03 2.2229e-03 0:00:30 420
81 4.1138e-04 6.5089e-05 1.7056e-05 2.9673e-03 1.2664e-03 2.1181e-03 0:00:29 419
82 3.8742e-04 6.0598e-05 1.5783e-05 2.6214e-03 1.1700e-03 2.0125e-03 0:01:15 418
83 3.6143e-04 5.6423e-05 1.4755e-05 2.2943e-03 1.0803e-03 1.9215e-03 0:01:06 417
84 3.4708e-04 5.2699e-05 1.3770e-05 1.9885e-03 9.9793e-04 1.8433e-03 0:00:59 416
85 3.2208e-04 4.9168e-05 1.2836e-05 1.7169e-03 9.1701e-04 1.7376e-03 0:00:53 415
86 2.9863e-04 4.5888e-05 1.1987e-05 1.4696e-03 8.3799e-04 1.6483e-03 0:00:48 414
87 2.7592e-04 4.2856e-05 1.1227e-05 1.2588e-03 7.6191e-04 1.5558e-03 0:00:44 413
88 2.5443e-04 4.0169e-05 1.0480e-05 1.0835e-03 7.0114e-04 1.4717e-03 0:00:41 412
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
89 2.3410e-04 3.7544e-05 9.8200e-06 9.3397e-04 6.4866e-04 1.3992e-03 0:00:39 411
90 2.1686e-04 3.5109e-05 9.2049e-06 8.0848e-04 5.9939e-04 1.3425e-03 0:00:37 410
91 2.0878e-04 3.2688e-05 8.6531e-06 7.0712e-04 5.5200e-04 1.3082e-03 0:00:35 409
92 1.9728e-04 3.0582e-05 8.1342e-06 6.2706e-04 5.0754e-04 1.2743e-03 0:00:34 408
93 1.8942e-04 2.8684e-05 7.6978e-06 5.6126e-04 4.6608e-04 1.2514e-03 0:00:33 407
94 1.8466e-04 2.7047e-05 7.3154e-06 5.0893e-04 4.2908e-04 1.2351e-03 0:00:32 406
95 1.8220e-04 2.5446e-05 7.0958e-06 4.6554e-04 3.9516e-04 1.2327e-03 0:00:31 405
96 1.8446e-04 2.3979e-05 6.8630e-06 4.2951e-04 3.6438e-04 1.2413e-03 0:00:30 404
97 1.9023e-04 2.2699e-05 6.5447e-06 3.9999e-04 3.3689e-04 1.2611e-03 0:00:30 403
98 1.9024e-04 2.1500e-05 6.3442e-06 3.7368e-04 3.1167e-04 1.2741e-03 0:00:29 402
99 1.9096e-04 2.0435e-05 6.2796e-06 3.5078e-04 2.9006e-04 1.2956e-03 0:00:29 401
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
100 1.9962e-04 1.9402e-05 6.2967e-06 3.3225e-04 2.7077e-04 1.3358e-03 0:00:29 400
101 2.0445e-04 1.8547e-05 6.3276e-06 3.1464e-04 2.5305e-04 1.3698e-03 0:00:29 399
102 2.0538e-04 1.7680e-05 6.3503e-06 2.9727e-04 2.3731e-04 1.3894e-03 0:00:29 398
103 2.0696e-04 1.6953e-05 6.2642e-06 2.8148e-04 2.2264e-04 1.4126e-03 0:00:29 397
104 2.0843e-04 1.6337e-05 6.2609e-06 2.6719e-04 2.0971e-04 1.4373e-03 0:00:29 396
105 2.0985e-04 1.5661e-05 6.1569e-06 2.5343e-04 1.9720e-04 1.4627e-03 0:00:29 395
106 2.1570e-04 1.5123e-05 6.0656e-06 2.4233e-04 1.8594e-04 1.5028e-03 0:00:29 394
107 2.1523e-04 1.4607e-05 6.1262e-06 2.3226e-04 1.7623e-04 1.5279e-03 0:00:29 393
108 2.1630e-04 1.4375e-05 6.1969e-06 2.2326e-04 1.6762e-04 1.5490e-03 0:00:29 392
109 2.1739e-04 1.4238e-05 6.2478e-06 1.9801e-04 1.5615e-04 1.5681e-03 0:00:28 391
110 2.2043e-04 1.4294e-05 6.1679e-06 1.9223e-04 1.4803e-04 1.5874e-03 0:00:28 390
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
111 2.2741e-04 1.4205e-05 6.2237e-06 1.8065e-04 1.4082e-04 1.6171e-03 0:00:27 389
112 2.2715e-04 1.3867e-05 6.2940e-06 1.7045e-04 1.3459e-04 1.6331e-03 0:00:27 388
113 2.2916e-04 1.3242e-05 6.3025e-06 1.6271e-04 1.2978e-04 1.6524e-03 0:00:27 387
114 2.3524e-04 1.2846e-05 6.1633e-06 1.5766e-04 1.2660e-04 1.6647e-03 0:00:27 386
115 2.3359e-04 1.2657e-05 6.0524e-06 1.5292e-04 1.2367e-04 1.6674e-03 0:00:26 385
116 2.3569e-04 1.2519e-05 5.8745e-06 1.4784e-04 1.2109e-04 1.6781e-03 0:00:26 384
117 2.3426e-04 1.2453e-05 5.9243e-06 1.4622e-04 1.1893e-04 1.6795e-03 0:00:26 383
118 2.3478e-04 1.2321e-05 5.9745e-06 1.4380e-04 1.1672e-04 1.6931e-03 0:00:26 382
119 2.3352e-04 1.2093e-05 6.0040e-06 1.4306e-04 1.1398e-04 1.6955e-03 0:00:26 381
120 2.3757e-04 1.1861e-05 5.8889e-06 1.4126e-04 1.1078e-04 1.7116e-03 0:00:26 380
121 2.3574e-04 1.1695e-05 5.6616e-06 1.4072e-04 1.0839e-04 1.7143e-03 0:00:27 379
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
122 2.3524e-04 1.1640e-05 5.5842e-06 1.3909e-04 1.0579e-04 1.7135e-03 0:00:27 378
123 2.3500e-04 1.1530e-05 5.6225e-06 1.3504e-04 1.0397e-04 1.7115e-03 0:00:26 377
124 2.3597e-04 1.1295e-05 5.6813e-06 1.2882e-04 1.0171e-04 1.7185e-03 0:00:26 376
125 2.3372e-04 1.1190e-05 5.6330e-06 1.2590e-04 1.0013e-04 1.7198e-03 0:00:26 375
126 2.3165e-04 1.1249e-05 5.6385e-06 1.2283e-04 9.9681e-05 1.7212e-03 0:00:26 374
127 2.4031e-04 1.1200e-05 5.6016e-06 1.2435e-04 1.0046e-04 1.7367e-03 0:00:26 373
128 2.3778e-04 1.1037e-05 5.3908e-06 1.2560e-04 1.0142e-04 1.7270e-03 0:00:26 372
129 2.3734e-04 1.0649e-05 5.2258e-06 1.2455e-04 1.0178e-04 1.7217e-03 0:00:25 371
130 2.3479e-04 1.0506e-05 5.0152e-06 1.3188e-04 1.0291e-04 1.7103e-03 0:00:25 370
131 2.3077e-04 1.0389e-05 4.8231e-06 1.2805e-04 1.0262e-04 1.7011e-03 0:00:25 369
132 2.2823e-04 1.0311e-05 4.7961e-06 1.2649e-04 1.0040e-04 1.6973e-03 0:00:25 368
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
133 2.3194e-04 1.0230e-05 4.8199e-06 1.2630e-04 9.7744e-05 1.7114e-03 0:00:26 367
134 2.3007e-04 1.0155e-05 4.6981e-06 1.2591e-04 9.6034e-05 1.7046e-03 0:00:26 366
135 2.2872e-04 1.0115e-05 4.3859e-06 1.2467e-04 9.4469e-05 1.7025e-03 0:00:26 365
136 2.2796e-04 1.0062e-05 4.3154e-06 1.2216e-04 9.3308e-05 1.6963e-03 0:00:26 364
137 2.2702e-04 9.9774e-06 4.3683e-06 1.1754e-04 9.2179e-05 1.6890e-03 0:00:26 363
138 2.3076e-04 9.8712e-06 4.3859e-06 1.1407e-04 9.1411e-05 1.6943e-03 0:00:26 362
139 2.2792e-04 9.7935e-06 4.3986e-06 1.1287e-04 9.1020e-05 1.6928e-03 0:00:26 361
140 2.2478e-04 9.9116e-06 4.4255e-06 1.1250e-04 9.1944e-05 1.6877e-03 0:00:26 360
141 2.3264e-04 9.9978e-06 4.3791e-06 1.1465e-04 9.3557e-05 1.6983e-03 0:00:26 359
142 2.2894e-04 9.9235e-06 4.2029e-06 1.1491e-04 9.4698e-05 1.6829e-03 0:00:26 358
143 2.3039e-04 9.5433e-06 4.0519e-06 1.1382e-04 9.4677e-05 1.6786e-03 0:00:26 357
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
144 2.2766e-04 9.4140e-06 3.8401e-06 1.1253e-04 9.3751e-05 1.6660e-03 0:00:26 356
145 2.2542e-04 9.5252e-06 3.8750e-06 1.1135e-04 9.2079e-05 1.6549e-03 0:00:26 355
146 2.2313e-04 9.5442e-06 3.9962e-06 1.1045e-04 9.0214e-05 1.6505e-03 0:00:26 354
147 2.2788e-04 9.5259e-06 4.0942e-06 1.1054e-04 8.7593e-05 1.6644e-03 0:00:26 353
148 2.2496e-04 9.5273e-06 3.9745e-06 1.1047e-04 8.6952e-05 1.6564e-03 0:00:25 352
149 2.2371e-04 9.5518e-06 3.6963e-06 1.1008e-04 8.5883e-05 1.6464e-03 0:00:25 351
150 2.2275e-04 9.4398e-06 3.6890e-06 1.0641e-04 8.5590e-05 1.6375e-03 0:00:26 350
151 2.2121e-04 9.4251e-06 3.7874e-06 1.0254e-04 8.4655e-05 1.6298e-03 0:00:25 349
152 2.2438e-04 9.3561e-06 3.8314e-06 1.0099e-04 8.4262e-05 1.6357e-03 0:00:25 348
153 2.2133e-04 9.3458e-06 3.8805e-06 1.0120e-04 8.4509e-05 1.6323e-03 0:00:25 347
154 2.1989e-04 9.4661e-06 3.9373e-06 1.0206e-04 8.5995e-05 1.6271e-03 0:00:24 346
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
155 2.2019e-04 9.5778e-06 3.8906e-06 1.0431e-04 8.7685e-05 1.6242e-03 0:00:24 345
156 2.1767e-04 9.4852e-06 3.7490e-06 1.0514e-04 8.8551e-05 1.6119e-03 0:00:24 344
157 2.2030e-04 9.1341e-06 3.6377e-06 1.0497e-04 8.8334e-05 1.6077e-03 0:00:24 343
158 2.1845e-04 9.0685e-06 3.4526e-06 1.0409e-04 8.7122e-05 1.5951e-03 0:00:24 342
159 2.1651e-04 9.2026e-06 3.5554e-06 1.0331e-04 8.5136e-05 1.5851e-03 0:00:24 341
160 2.1433e-04 9.2366e-06 3.6990e-06 1.0321e-04 8.3075e-05 1.5804e-03 0:00:24 340
161 2.1912e-04 9.2332e-06 3.7836e-06 1.0331e-04 8.0578e-05 1.5926e-03 0:00:23 339
162 2.1693e-04 9.2198e-06 3.6666e-06 1.0333e-04 8.0394e-05 1.5853e-03 0:00:24 338
163 2.1586e-04 9.2424e-06 3.4310e-06 1.0218e-04 7.9125e-05 1.5754e-03 0:00:24 337
164 2.1512e-04 9.1258e-06 3.4457e-06 9.8169e-05 7.8953e-05 1.5673e-03 0:00:24 336
165 2.1373e-04 9.1035e-06 3.5472e-06 9.3759e-05 7.8148e-05 1.5584e-03 0:00:24 335
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
166 2.1713e-04 9.0264e-06 3.6092e-06 9.2494e-05 7.8033e-05 1.5624e-03 0:00:23 334
167 2.1431e-04 8.9654e-06 3.6691e-06 9.3197e-05 7.8703e-05 1.5580e-03 0:00:24 333
168 2.1112e-04 9.0771e-06 3.7426e-06 9.4754e-05 8.0447e-05 1.5499e-03 0:00:24 332
169 2.1802e-04 9.2282e-06 3.7155e-06 9.7409e-05 8.2212e-05 1.5568e-03 0:00:24 331
170 2.1463e-04 9.1833e-06 3.5743e-06 9.8494e-05 8.3525e-05 1.5435e-03 0:00:24 330
171 2.1564e-04 8.8446e-06 3.4737e-06 9.8344e-05 8.3677e-05 1.5366e-03 0:00:24 329
172 2.1331e-04 8.7462e-06 3.2866e-06 9.7532e-05 8.2861e-05 1.5224e-03 0:00:24 328
173 2.1110e-04 8.8803e-06 3.3949e-06 9.6623e-05 8.1464e-05 1.5121e-03 0:00:24 327
174 2.0886e-04 8.9222e-06 3.5104e-06 9.5843e-05 7.9804e-05 1.5065e-03 0:00:24 326
175 2.1181e-04 8.9153e-06 3.6239e-06 9.6003e-05 7.7484e-05 1.5140e-03 0:00:24 325
176 2.0987e-04 8.8939e-06 3.5528e-06 9.6466e-05 7.7354e-05 1.5079e-03 0:00:24 324
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
177 2.0915e-04 8.8964e-06 3.3147e-06 9.5807e-05 7.6571e-05 1.5002e-03 0:00:23 323
178 2.0853e-04 8.9134e-06 3.2476e-06 9.2988e-05 7.6210e-05 1.4912e-03 0:00:23 322
179 2.0754e-04 8.8704e-06 3.3736e-06 8.8931e-05 7.5747e-05 1.4821e-03 0:00:23 321
180 2.0881e-04 8.7924e-06 3.4943e-06 8.7017e-05 7.5590e-05 1.4807e-03 0:00:22 320
181 2.0655e-04 8.7000e-06 3.5150e-06 8.7802e-05 7.5731e-05 1.4769e-03 0:00:23 319
182 2.0435e-04 8.8012e-06 3.6072e-06 8.8608e-05 7.6878e-05 1.4747e-03 0:00:23 318
183 2.1052e-04 8.8727e-06 3.6533e-06 9.0496e-05 7.8328e-05 1.4810e-03 0:00:23 317
184 2.0719e-04 8.9916e-06 3.5286e-06 9.1994e-05 7.9540e-05 1.4681e-03 0:00:23 316
185 2.0468e-04 8.8403e-06 3.4095e-06 9.2214e-05 8.0016e-05 1.4559e-03 0:00:23 315
186 2.0708e-04 8.5456e-06 3.3093e-06 9.1576e-05 7.9547e-05 1.4524e-03 0:00:23 314
187 2.0500e-04 8.5094e-06 3.2249e-06 9.0408e-05 7.8241e-05 1.4398e-03 0:00:23 313
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
188 2.0275e-04 8.6591e-06 3.3391e-06 8.9780e-05 7.6695e-05 1.4315e-03 0:00:23 312
189 2.0274e-04 8.6698e-06 3.4528e-06 8.9316e-05 7.4933e-05 1.4326e-03 0:00:23 311
190 2.0470e-04 8.6354e-06 3.4859e-06 8.9679e-05 7.3189e-05 1.4350e-03 0:00:23 310
191 2.0323e-04 8.6113e-06 3.3931e-06 8.9952e-05 7.3291e-05 1.4276e-03 0:00:23 309
192 2.0241e-04 8.6133e-06 3.1579e-06 8.9366e-05 7.2303e-05 1.4215e-03 0:00:23 308
193 2.0172e-04 8.6392e-06 3.1655e-06 8.5834e-05 7.2024e-05 1.4111e-03 0:00:22 307
194 2.0050e-04 8.5871e-06 3.2910e-06 8.1503e-05 7.1635e-05 1.4021e-03 0:00:22 306
195 1.9909e-04 8.4449e-06 3.4260e-06 7.9882e-05 7.1563e-05 1.3954e-03 0:00:22 305
196 2.0073e-04 8.3628e-06 3.4219e-06 8.1147e-05 7.2090e-05 1.3981e-03 0:00:22 304
197 1.9835e-04 8.4654e-06 3.5003e-06 8.2395e-05 7.3082e-05 1.3942e-03 0:00:22 303
198 2.0060e-04 8.5196e-06 3.5357e-06 8.4372e-05 7.4363e-05 1.3963e-03 0:00:21 302
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
199 1.9800e-04 8.6713e-06 3.4431e-06 8.5314e-05 7.5327e-05 1.3853e-03 0:00:21 301
200 1.9561e-04 8.5708e-06 3.3066e-06 8.5783e-05 7.5971e-05 1.3744e-03 0:00:21 300
201 1.9723e-04 8.3012e-06 3.2459e-06 8.5509e-05 7.5629e-05 1.3706e-03 0:00:51 299
202 1.9559e-04 8.2529e-06 3.1352e-06 8.4551e-05 7.4354e-05 1.3568e-03 0:00:45 298
203 1.9374e-04 8.3611e-06 3.2365e-06 8.3964e-05 7.2871e-05 1.3489e-03 0:00:41 297
204 1.9393e-04 8.4161e-06 3.3329e-06 8.3533e-05 7.1279e-05 1.3485e-03 0:00:37 296
205 1.9262e-04 8.3839e-06 3.3981e-06 8.2916e-05 6.9278e-05 1.3422e-03 0:00:34 295
206 1.9625e-04 8.3245e-06 3.2740e-06 8.3383e-05 6.9538e-05 1.3471e-03 0:00:31 294
207 1.9539e-04 8.2859e-06 3.1244e-06 8.3076e-05 6.8984e-05 1.3426e-03 0:00:30 293
208 1.9458e-04 8.3151e-06 3.0156e-06 8.0488e-05 6.8055e-05 1.3351e-03 0:00:28 292
209 1.9340e-04 8.2519e-06 3.1060e-06 7.6339e-05 6.7781e-05 1.3248e-03 0:00:27 291
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
210 1.9183e-04 8.1871e-06 3.2375e-06 7.3189e-05 6.7664e-05 1.3161e-03 0:00:26 290
211 1.9349e-04 8.0614e-06 3.3368e-06 7.3340e-05 6.8127e-05 1.3158e-03 0:00:25 289
212 1.9138e-04 7.9880e-06 3.3155e-06 7.5146e-05 6.9157e-05 1.3102e-03 0:00:24 288
213 1.8917e-04 8.1103e-06 3.3916e-06 7.7245e-05 6.9945e-05 1.3063e-03 0:00:23 287
214 1.9420e-04 8.1621e-06 3.3962e-06 7.9201e-05 7.1105e-05 1.3136e-03 0:00:22 286
215 1.9137e-04 8.3079e-06 3.2986e-06 7.9684e-05 7.1839e-05 1.3015e-03 0:00:22 285
216 1.8872e-04 8.2303e-06 3.2119e-06 7.9318e-05 7.2278e-05 1.2902e-03 0:00:21 284
217 1.8903e-04 7.9971e-06 3.1434e-06 7.8661e-05 7.1864e-05 1.2842e-03 0:00:21 283
218 1.8712e-04 7.9494e-06 3.0328e-06 7.7714e-05 7.0752e-05 1.2728e-03 0:00:21 282
219 1.8503e-04 8.0283e-06 3.1207e-06 7.7180e-05 6.9461e-05 1.2652e-03 0:00:21 281
220 1.8542e-04 8.1073e-06 3.1970e-06 7.7053e-05 6.8128e-05 1.2625e-03 0:00:21 280
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
221 1.8431e-04 8.0636e-06 3.2580e-06 7.6487e-05 6.5827e-05 1.2557e-03 0:00:36 279
222 1.8690e-04 7.9762e-06 3.1529e-06 7.6501e-05 6.6296e-05 1.2578e-03 0:00:33 278
223 1.8581e-04 7.9409e-06 3.0376e-06 7.6391e-05 6.5815e-05 1.2534e-03 0:00:30 277
224 1.8503e-04 7.9358e-06 2.8702e-06 7.4931e-05 6.4840e-05 1.2480e-03 0:00:28 276
225 1.8402e-04 7.9423e-06 2.9010e-06 7.1040e-05 6.4710e-05 1.2387e-03 0:00:26 275
226 1.8261e-04 7.8150e-06 3.0641e-06 6.7147e-05 6.4500e-05 1.2288e-03 0:00:24 274
227 1.8137e-04 7.7307e-06 3.1646e-06 6.6591e-05 6.4817e-05 1.2216e-03 0:00:23 273
228 1.8426e-04 7.6477e-06 3.2080e-06 6.8461e-05 6.5885e-05 1.2247e-03 0:00:22 272
229 1.8192e-04 7.6235e-06 3.2043e-06 7.0707e-05 6.6735e-05 1.2195e-03 0:00:22 271
230 1.8013e-04 7.7184e-06 3.2742e-06 7.2590e-05 6.7298e-05 1.2159e-03 0:00:22 270
231 1.8652e-04 7.7773e-06 3.2324e-06 7.3620e-05 6.7898e-05 1.2249e-03 0:00:21 269
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
232 1.8333e-04 7.9322e-06 3.1605e-06 7.3872e-05 6.8388e-05 1.2119e-03 0:00:21 268
233 1.8042e-04 7.8680e-06 3.0647e-06 7.3212e-05 6.8681e-05 1.2009e-03 0:00:21 267
234 1.7942e-04 7.6761e-06 2.9733e-06 7.1992e-05 6.7870e-05 1.1938e-03 0:00:20 266
235 1.7728e-04 7.6140e-06 2.8893e-06 7.0737e-05 6.6661e-05 1.1827e-03 0:00:20 265
236 1.7496e-04 7.6524e-06 2.9681e-06 7.0295e-05 6.5433e-05 1.1743e-03 0:00:19 264
237 1.7524e-04 7.7532e-06 3.0468e-06 7.0409e-05 6.4314e-05 1.1691e-03 0:00:19 263
238 1.7444e-04 7.7040e-06 3.1066e-06 6.9923e-05 6.2238e-05 1.1614e-03 0:00:19 262
239 1.7348e-04 7.6082e-06 3.0123e-06 6.9579e-05 6.2692e-05 1.1571e-03 0:00:19 261
240 1.7667e-04 7.5449e-06 2.8939e-06 6.9672e-05 6.2453e-05 1.1607e-03 0:00:19 260
241 1.7571e-04 7.5594e-06 2.7896e-06 6.9345e-05 6.1659e-05 1.1552e-03 0:00:19 259
242 1.7442e-04 7.4896e-06 2.7267e-06 6.5882e-05 6.0998e-05 1.1478e-03 0:00:19 258
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
243 1.7296e-04 7.4026e-06 2.8313e-06 6.1398e-05 6.0559e-05 1.1385e-03 0:00:19 257
244 1.7154e-04 7.3374e-06 2.9576e-06 5.9978e-05 6.0786e-05 1.1297e-03 0:00:18 256
245 1.7027e-04 7.2578e-06 3.0531e-06 6.1069e-05 6.1760e-05 1.1239e-03 0:00:18 255
246 1.7286e-04 7.1994e-06 3.0766e-06 6.3746e-05 6.3083e-05 1.1266e-03 0:00:19 254
247 1.7086e-04 7.2273e-06 3.0743e-06 6.5310e-05 6.3664e-05 1.1213e-03 0:00:19 253
248 1.6920e-04 7.2704e-06 3.1276e-06 6.6736e-05 6.3775e-05 1.1169e-03 0:00:19 252
249 1.7402e-04 7.3155e-06 3.0840e-06 6.7490e-05 6.3881e-05 1.1251e-03 0:00:18 251
250 1.7117e-04 7.5011e-06 3.0385e-06 6.7667e-05 6.4017e-05 1.1126e-03 0:00:18 250
251 1.6853e-04 7.4825e-06 2.8999e-06 6.6907e-05 6.4060e-05 1.1022e-03 0:00:18 249
252 1.6606e-04 7.2933e-06 2.8188e-06 6.5337e-05 6.2992e-05 1.0919e-03 0:00:18 248
253 1.6732e-04 7.2196e-06 2.7292e-06 6.4267e-05 6.1972e-05 1.0901e-03 0:00:18 247
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
254 1.6470e-04 7.2360e-06 2.8014e-06 6.3459e-05 6.0857e-05 1.0803e-03 0:00:18 246
255 1.6475e-04 7.3058e-06 2.8551e-06 6.3576e-05 5.9757e-05 1.0730e-03 0:00:18 245
256 1.6365e-04 7.3125e-06 2.9073e-06 6.3924e-05 5.8416e-05 1.0630e-03 0:00:18 244
257 1.6264e-04 7.2044e-06 2.8601e-06 6.3239e-05 5.8279e-05 1.0576e-03 0:00:18 243
258 1.6160e-04 7.1064e-06 2.7784e-06 6.2769e-05 5.8101e-05 1.0538e-03 0:00:17 242
259 1.6449e-04 7.0851e-06 2.6878e-06 6.2098e-05 5.7537e-05 1.0554e-03 0:00:17 241
260 1.6319e-04 7.0764e-06 2.6070e-06 6.1296e-05 5.6813e-05 1.0481e-03 0:00:17 240
261 1.6163e-04 6.9439e-06 2.5747e-06 5.7131e-05 5.6552e-05 1.0406e-03 0:00:17 239
262 1.6006e-04 6.8426e-06 2.7006e-06 5.3195e-05 5.6021e-05 1.0325e-03 0:00:17 238
263 1.5866e-04 6.7891e-06 2.7903e-06 5.2794e-05 5.6444e-05 1.0242e-03 0:00:17 237
264 1.5737e-04 6.7219e-06 2.8201e-06 5.4982e-05 5.7972e-05 1.0171e-03 0:00:17 236
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
265 1.5621e-04 6.6679e-06 2.8631e-06 5.7998e-05 5.9465e-05 1.0129e-03 0:00:17 235
266 1.5833e-04 6.6529e-06 2.8718e-06 6.0045e-05 6.0162e-05 1.0140e-03 0:00:17 234
267 1.5679e-04 6.7332e-06 2.9473e-06 6.0726e-05 6.0114e-05 1.0096e-03 0:00:17 233
268 1.5531e-04 6.7448e-06 2.9445e-06 6.1255e-05 5.9891e-05 1.0065e-03 0:00:17 232
269 1.6107e-04 6.8548e-06 2.8680e-06 6.1821e-05 5.9692e-05 1.0149e-03 0:00:16 231
270 1.5801e-04 7.0062e-06 2.8041e-06 6.1467e-05 5.9611e-05 1.0029e-03 0:00:16 230
271 1.5529e-04 6.9513e-06 2.6859e-06 6.0058e-05 5.9070e-05 9.9201e-04 0:00:16 229
272 1.5267e-04 6.7550e-06 2.5857e-06 5.8163e-05 5.8091e-05 9.8237e-04 0:00:16 228
273 1.5339e-04 6.6849e-06 2.5210e-06 5.7096e-05 5.7551e-05 9.8049e-04 0:00:16 227
274 1.5251e-04 6.7203e-06 2.6088e-06 5.6295e-05 5.6648e-05 9.7311e-04 0:00:16 226
275 1.5048e-04 6.7369e-06 2.6480e-06 5.6180e-05 5.5565e-05 9.6165e-04 0:00:16 225
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
276 1.4959e-04 6.7848e-06 2.6868e-06 5.6191e-05 5.4419e-05 9.5206e-04 0:00:16 224
277 1.4846e-04 6.6648e-06 2.6273e-06 5.5944e-05 5.3827e-05 9.4534e-04 0:00:16 223
278 1.4750e-04 6.5766e-06 2.5403e-06 5.5746e-05 5.3711e-05 9.3931e-04 0:00:16 222
279 1.4687e-04 6.5386e-06 2.4620e-06 5.5170e-05 5.3614e-05 9.3528e-04 0:00:16 221
280 1.4737e-04 6.5060e-06 2.4599e-06 5.3820e-05 5.3205e-05 9.3187e-04 0:00:16 220
281 1.4611e-04 6.4377e-06 2.4207e-06 5.2068e-05 5.2660e-05 9.2598e-04 0:00:15 219
282 1.4495e-04 6.2915e-06 2.3881e-06 4.8352e-05 5.2314e-05 9.1907e-04 0:00:15 218
283 1.4365e-04 6.1812e-06 2.5049e-06 4.5781e-05 5.1925e-05 9.1142e-04 0:00:15 217
284 1.4245e-04 6.1214e-06 2.6102e-06 4.6688e-05 5.2446e-05 9.0519e-04 0:00:15 216
285 1.4138e-04 6.0950e-06 2.5922e-06 4.9458e-05 5.3988e-05 8.9948e-04 0:00:15 215
286 1.4044e-04 6.0289e-06 2.6102e-06 5.2188e-05 5.5495e-05 8.9422e-04 0:00:15 214
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
287 1.4110e-04 6.0281e-06 2.6556e-06 5.3905e-05 5.6385e-05 8.9228e-04 0:00:15 213
288 1.4012e-04 6.0770e-06 2.7176e-06 5.4455e-05 5.6059e-05 8.8769e-04 0:00:15 212
289 1.3902e-04 6.1029e-06 2.6994e-06 5.4204e-05 5.5373e-05 8.8417e-04 0:00:14 211
290 1.3789e-04 6.1518e-06 2.6016e-06 5.4052e-05 5.4680e-05 8.8132e-04 0:00:15 210
291 1.4123e-04 6.2514e-06 2.5523e-06 5.4225e-05 5.4214e-05 8.8578e-04 0:00:15 209
292 1.3882e-04 6.3905e-06 2.5251e-06 5.4368e-05 5.4071e-05 8.7757e-04 0:00:14 208
293 1.3660e-04 6.3583e-06 2.4750e-06 5.3057e-05 5.3053e-05 8.6783e-04 0:00:14 207
294 1.3459e-04 6.1399e-06 2.3671e-06 5.1387e-05 5.2048e-05 8.5861e-04 0:00:14 206
295 1.3276e-04 6.0357e-06 2.2828e-06 4.9922e-05 5.1154e-05 8.5031e-04 0:00:14 205
296 1.3374e-04 6.0698e-06 2.3542e-06 4.8861e-05 5.0322e-05 8.4706e-04 0:00:14 204
297 1.3317e-04 6.1170e-06 2.3942e-06 4.7887e-05 4.9457e-05 8.4126e-04 0:00:14 203
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
298 1.3202e-04 6.0846e-06 2.4044e-06 4.7468e-05 4.8392e-05 8.3131e-04 0:00:14 202
299 1.3081e-04 6.0563e-06 2.3904e-06 4.7183e-05 4.7596e-05 8.2246e-04 0:00:14 201
300 1.3009e-04 5.9354e-06 2.3050e-06 4.6732e-05 4.7673e-05 8.1400e-04 0:00:14 200
301 1.2939e-04 5.8461e-06 2.2453e-06 4.6223e-05 4.7598e-05 8.0777e-04 0:00:14 199
302 1.2872e-04 5.7876e-06 2.1754e-06 4.5354e-05 4.7359e-05 8.0198e-04 0:00:13 198
303 1.2999e-04 5.7127e-06 2.1558e-06 4.4278e-05 4.7097e-05 8.0174e-04 0:00:14 197
304 1.2848e-04 5.6450e-06 2.1570e-06 4.3051e-05 4.6818e-05 7.9531e-04 0:00:14 196
305 1.2721e-04 5.5499e-06 2.1181e-06 4.1144e-05 4.6731e-05 7.8706e-04 0:00:14 195
306 1.2586e-04 5.4344e-06 2.0980e-06 3.9195e-05 4.6455e-05 7.7942e-04 0:00:14 194
307 1.2453e-04 5.3363e-06 2.2022e-06 3.9110e-05 4.6640e-05 7.7333e-04 0:00:14 193
308 1.2330e-04 5.2622e-06 2.3116e-06 4.1343e-05 4.8244e-05 7.6760e-04 0:00:14 192
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
309 1.2237e-04 5.2830e-06 2.2923e-06 4.3728e-05 4.9845e-05 7.6272e-04 0:00:14 191
310 1.2160e-04 5.2545e-06 2.3226e-06 4.5810e-05 5.1175e-05 7.5836e-04 0:00:14 190
311 1.2098e-04 5.2391e-06 2.3601e-06 4.7036e-05 5.2152e-05 7.5264e-04 0:00:13 189
312 1.2016e-04 5.2667e-06 2.4144e-06 4.7734e-05 5.2030e-05 7.4740e-04 0:00:13 188
313 1.2215e-04 5.3408e-06 2.4446e-06 4.7961e-05 5.1168e-05 7.4844e-04 0:00:13 187
314 1.2048e-04 5.3552e-06 2.3875e-06 4.7154e-05 5.0018e-05 7.4358e-04 0:00:13 186
315 1.1882e-04 5.3798e-06 2.2514e-06 4.6355e-05 4.9160e-05 7.3872e-04 0:00:13 185
316 1.1922e-04 5.4486e-06 2.1914e-06 4.6052e-05 4.8596e-05 7.3747e-04 0:00:13 184
317 1.1750e-04 5.5371e-06 2.1611e-06 4.5932e-05 4.7789e-05 7.3137e-04 0:00:13 183
318 1.1741e-04 5.6112e-06 2.1437e-06 4.5589e-05 4.6699e-05 7.2685e-04 0:00:13 182
319 1.1536e-04 5.5234e-06 2.1047e-06 4.4550e-05 4.5678e-05 7.1885e-04 0:00:31 181
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
320 1.1367e-04 5.3345e-06 2.0077e-06 4.2734e-05 4.4749e-05 7.1015e-04 0:00:27 180
321 1.1203e-04 5.1790e-06 1.9316e-06 4.0788e-05 4.3786e-05 7.0180e-04 0:00:24 179
322 1.1180e-04 5.2067e-06 1.9829e-06 3.9295e-05 4.3089e-05 6.9676e-04 0:00:22 178
323 1.1138e-04 5.2145e-06 2.0217e-06 3.8084e-05 4.2536e-05 6.9159e-04 0:00:20 177
324 1.1007e-04 5.2087e-06 2.0511e-06 3.7209e-05 4.1833e-05 6.8265e-04 0:00:19 176
325 1.0889e-04 5.1284e-06 2.0611e-06 3.6430e-05 4.1379e-05 6.7382e-04 0:00:18 175
326 1.0798e-04 5.0631e-06 2.0123e-06 3.6025e-05 4.0893e-05 6.6529e-04 0:00:17 174
327 1.0713e-04 4.9910e-06 1.9353e-06 3.5962e-05 4.0713e-05 6.5700e-04 0:00:16 173
328 1.0647e-04 4.8888e-06 1.8851e-06 3.5794e-05 4.0711e-05 6.5009e-04 0:00:15 172
329 1.0571e-04 4.8256e-06 1.8492e-06 3.5450e-05 4.0637e-05 6.4436e-04 0:00:14 171
330 1.0474e-04 4.7350e-06 1.7841e-06 3.5169e-05 4.0481e-05 6.3829e-04 0:00:14 170
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
331 1.0371e-04 4.6654e-06 1.7710e-06 3.4736e-05 4.0346e-05 6.3181e-04 0:00:13 169
332 1.0472e-04 4.6141e-06 1.7670e-06 3.4296e-05 4.0079e-05 6.3019e-04 0:00:13 168
333 1.0338e-04 4.5518e-06 1.7371e-06 3.3339e-05 3.9883e-05 6.2383e-04 0:00:13 167
334 1.0205e-04 4.4805e-06 1.7275e-06 3.2031e-05 4.0010e-05 6.1674e-04 0:00:12 166
335 1.0069e-04 4.4101e-06 1.7188e-06 3.1621e-05 4.0266e-05 6.1035e-04 0:00:12 165
336 9.9504e-05 4.3335e-06 1.8226e-06 3.2286e-05 4.1165e-05 6.0483e-04 0:00:12 164
337 9.8446e-05 4.2429e-06 1.9150e-06 3.4226e-05 4.2150e-05 6.0018e-04 0:00:12 163
338 9.7491e-05 4.2676e-06 1.9739e-06 3.6208e-05 4.3349e-05 5.9508e-04 0:00:12 162
339 9.6755e-05 4.2848e-06 1.9720e-06 3.7548e-05 4.4120e-05 5.8957e-04 0:00:11 161
340 9.6057e-05 4.2692e-06 1.9949e-06 3.8050e-05 4.4458e-05 5.8406e-04 0:00:11 160
341 9.5250e-05 4.2581e-06 1.9711e-06 3.8050e-05 4.4527e-05 5.7900e-04 0:00:11 159
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
342 9.4407e-05 4.2480e-06 1.9692e-06 3.7945e-05 4.4585e-05 5.7633e-04 0:00:11 158
343 9.3723e-05 4.2930e-06 2.0384e-06 3.8637e-05 4.3602e-05 5.7297e-04 0:00:11 157
344 9.3083e-05 4.4158e-06 2.0660e-06 3.8488e-05 4.3077e-05 5.6950e-04 0:00:11 156
345 9.4632e-05 4.4062e-06 2.0286e-06 3.7536e-05 4.1938e-05 5.6943e-04 0:00:11 155
346 9.3305e-05 4.4037e-06 1.9543e-06 3.6162e-05 4.1265e-05 5.6417e-04 0:00:11 154
347 9.1784e-05 4.4421e-06 1.8433e-06 3.4803e-05 3.9627e-05 5.5679e-04 0:00:11 153
348 9.0287e-05 4.4436e-06 1.7384e-06 3.3745e-05 3.8359e-05 5.5056e-04 0:00:11 152
349 8.8353e-05 4.4120e-06 1.6799e-06 3.3111e-05 3.6701e-05 5.4308e-04 0:00:10 151
350 8.6651e-05 4.3606e-06 1.6606e-06 3.2981e-05 3.5735e-05 5.3625e-04 0:00:10 150
351 8.7856e-05 4.3008e-06 1.6451e-06 3.2763e-05 3.5029e-05 5.3317e-04 0:00:10 149
352 8.6125e-05 4.1647e-06 1.5796e-06 3.1868e-05 3.4669e-05 5.2619e-04 0:00:10 148
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
353 8.4775e-05 4.0130e-06 1.5177e-06 3.0249e-05 3.4240e-05 5.1981e-04 0:00:10 147
354 8.3474e-05 3.9504e-06 1.4609e-06 2.8663e-05 3.3865e-05 5.1206e-04 0:00:10 146
355 8.2290e-05 3.9357e-06 1.4691e-06 2.7521e-05 3.3590e-05 5.0405e-04 0:00:10 145
356 8.0911e-05 3.9019e-06 1.4846e-06 2.6913e-05 3.3431e-05 4.9744e-04 0:00:10 144
357 8.0560e-05 3.8784e-06 1.5044e-06 2.6762e-05 3.3352e-05 4.9212e-04 0:00:10 143
358 8.1097e-05 3.8420e-06 1.5243e-06 2.6783e-05 3.3293e-05 4.8716e-04 0:00:10 142
359 7.9763e-05 3.7575e-06 1.5359e-06 2.7035e-05 3.3172e-05 4.7932e-04 0:00:10 141
360 7.8476e-05 3.6772e-06 1.5162e-06 2.7195e-05 3.2986e-05 4.7219e-04 0:00:10 140
361 7.7356e-05 3.6135e-06 1.4333e-06 2.7157e-05 3.2779e-05 4.6509e-04 0:00:10 139
362 7.6354e-05 3.5841e-06 1.3747e-06 2.7083e-05 3.2258e-05 4.5801e-04 0:00:10 138
363 7.5326e-05 3.5749e-06 1.3277e-06 2.6490e-05 3.1641e-05 4.5048e-04 0:00:10 137
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
364 7.4324e-05 3.5724e-06 1.3023e-06 2.6006e-05 3.1386e-05 4.4339e-04 0:00:10 136
365 7.3409e-05 3.4906e-06 1.2832e-06 2.5674e-05 3.1250e-05 4.3627e-04 0:00:10 135
366 7.2469e-05 3.4125e-06 1.2689e-06 2.5324e-05 3.1086e-05 4.2996e-04 0:00:10 134
367 7.1534e-05 3.3525e-06 1.2292e-06 2.4980e-05 3.0884e-05 4.2450e-04 0:00:10 133
368 7.0534e-05 3.3039e-06 1.2143e-06 2.4744e-05 3.0645e-05 4.1932e-04 0:00:10 132
369 6.9481e-05 3.2570e-06 1.2137e-06 2.4526e-05 3.0399e-05 4.1428e-04 0:00:10 131
370 6.8431e-05 3.2120e-06 1.2065e-06 2.4180e-05 3.0139e-05 4.0905e-04 0:00:09 130
371 6.7387e-05 3.1675e-06 1.1974e-06 2.3830e-05 2.9963e-05 4.0406e-04 0:00:09 129
372 6.6470e-05 3.1195e-06 1.1829e-06 2.3509e-05 2.9639e-05 3.9930e-04 0:00:09 128
373 6.7027e-05 3.0512e-06 1.1858e-06 2.3198e-05 2.9777e-05 3.9642e-04 0:00:09 127
374 6.5970e-05 2.9840e-06 1.1876e-06 2.2604e-05 2.9906e-05 3.9034e-04 0:00:09 126
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
375 6.4980e-05 2.9184e-06 1.2098e-06 2.2740e-05 3.0507e-05 3.8420e-04 0:00:09 125
376 6.4063e-05 2.8688e-06 1.2769e-06 2.3676e-05 3.1135e-05 3.7838e-04 0:00:09 124
377 6.3185e-05 2.8378e-06 1.3500e-06 2.4843e-05 3.1909e-05 3.7290e-04 0:00:09 123
378 6.2340e-05 2.8145e-06 1.4075e-06 2.5550e-05 3.2534e-05 3.6768e-04 0:00:09 122
379 6.1549e-05 2.7991e-06 1.4522e-06 2.5841e-05 3.3177e-05 3.6333e-04 0:00:09 121
380 6.0878e-05 2.8178e-06 1.4664e-06 2.6210e-05 3.3038e-05 3.5911e-04 0:00:09 120
381 6.0309e-05 2.8347e-06 1.4551e-06 2.6428e-05 3.3077e-05 3.5475e-04 0:00:09 119
382 5.9606e-05 2.8412e-06 1.4576e-06 2.6017e-05 3.2767e-05 3.4986e-04 0:00:09 118
383 5.8798e-05 2.8546e-06 1.3883e-06 2.5320e-05 3.2148e-05 3.4591e-04 0:00:08 117
384 5.8011e-05 2.8304e-06 1.3520e-06 2.4368e-05 3.1267e-05 3.4093e-04 0:00:08 116
385 5.7263e-05 2.7815e-06 1.3467e-06 2.3283e-05 3.0494e-05 3.3653e-04 0:00:08 115
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
386 5.6462e-05 2.7395e-06 1.3529e-06 2.2199e-05 2.9739e-05 3.3215e-04 0:00:08 114
387 5.5667e-05 2.7092e-06 1.3455e-06 2.0995e-05 2.8584e-05 3.2726e-04 0:00:08 113
388 5.4766e-05 2.6740e-06 1.3088e-06 2.0195e-05 2.7913e-05 3.2234e-04 0:00:08 112
389 5.3812e-05 2.6456e-06 1.2753e-06 1.9834e-05 2.7185e-05 3.1749e-04 0:00:08 111
390 5.2809e-05 2.6314e-06 1.2280e-06 1.9747e-05 2.6622e-05 3.1249e-04 0:00:08 110
391 5.1833e-05 2.6161e-06 1.1635e-06 1.9662e-05 2.6103e-05 3.0716e-04 0:00:08 109
392 5.0825e-05 2.5730e-06 1.1149e-06 1.9317e-05 2.5489e-05 3.0202e-04 0:00:07 108
393 4.9793e-05 2.5447e-06 1.0667e-06 1.9174e-05 2.4802e-05 2.9680e-04 0:00:07 107
394 4.8688e-05 2.5623e-06 1.0207e-06 1.8953e-05 2.4202e-05 2.9135e-04 0:00:07 106
395 4.7660e-05 2.5666e-06 9.6355e-07 1.8739e-05 2.3346e-05 2.8562e-04 0:00:07 105
396 4.6552e-05 2.4931e-06 8.7865e-07 1.8522e-05 2.2888e-05 2.7993e-04 0:00:07 104
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
397 4.5569e-05 2.4139e-06 8.3318e-07 1.8475e-05 2.2351e-05 2.7462e-04 0:00:07 103
398 4.5429e-05 2.3500e-06 8.2311e-07 1.8608e-05 2.2003e-05 2.7067e-04 0:00:07 102
399 4.4366e-05 2.2842e-06 8.1630e-07 1.8794e-05 2.1743e-05 2.6526e-04 0:00:07 101
400 4.3381e-05 2.2211e-06 8.1469e-07 1.8866e-05 2.1528e-05 2.5987e-04 0:00:07 100
401 4.2502e-05 2.1600e-06 8.1718e-07 1.8772e-05 2.1356e-05 2.5479e-04 0:00:07 99
402 4.1678e-05 2.1281e-06 8.1960e-07 1.8576e-05 2.1128e-05 2.4980e-04 0:00:07 98
403 4.0656e-05 2.0988e-06 8.2323e-07 1.8258e-05 2.0854e-05 2.4439e-04 0:00:07 97
404 3.9686e-05 2.0613e-06 8.2488e-07 1.7943e-05 2.0639e-05 2.3953e-04 0:00:07 96
405 3.8834e-05 2.0309e-06 8.3781e-07 1.7480e-05 2.0150e-05 2.3489e-04 0:00:07 95
406 3.8080e-05 2.0001e-06 8.1857e-07 1.6940e-05 1.9921e-05 2.3026e-04 0:00:07 94
407 3.7266e-05 1.9738e-06 7.8935e-07 1.6225e-05 1.9580e-05 2.2587e-04 0:00:07 93
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
408 3.6554e-05 1.9365e-06 7.5919e-07 1.5577e-05 1.9202e-05 2.2110e-04 0:00:06 92
409 3.5908e-05 1.8729e-06 7.2338e-07 1.5027e-05 1.8909e-05 2.1637e-04 0:00:07 91
410 3.5233e-05 1.8169e-06 6.9773e-07 1.4637e-05 1.8639e-05 2.1161e-04 0:00:07 90
411 3.4510e-05 1.7799e-06 6.9266e-07 1.4408e-05 1.8404e-05 2.0702e-04 0:00:06 89
412 3.3752e-05 1.7403e-06 6.8748e-07 1.4210e-05 1.8192e-05 2.0251e-04 0:00:06 88
413 3.2979e-05 1.7004e-06 6.8117e-07 1.4110e-05 1.7993e-05 1.9802e-04 0:00:06 87
414 3.2220e-05 1.6610e-06 6.7020e-07 1.4067e-05 1.7798e-05 1.9343e-04 0:00:06 86
415 3.1506e-05 1.6237e-06 6.6221e-07 1.3990e-05 1.7594e-05 1.8895e-04 0:00:06 85
416 3.1449e-05 1.5912e-06 6.4963e-07 1.3892e-05 1.7277e-05 1.8485e-04 0:00:06 84
417 3.0457e-05 1.5532e-06 6.2528e-07 1.3739e-05 1.7241e-05 1.7963e-04 0:00:06 83
418 2.9611e-05 1.5196e-06 6.0657e-07 1.3661e-05 1.6863e-05 1.7462e-04 0:00:06 82
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
419 2.8825e-05 1.4869e-06 5.8944e-07 1.3446e-05 1.6612e-05 1.6970e-04 0:00:06 81
420 2.8074e-05 1.4545e-06 5.7400e-07 1.3222e-05 1.6451e-05 1.6530e-04 0:00:06 80
421 2.7351e-05 1.4306e-06 5.6977e-07 1.3180e-05 1.6192e-05 1.6089e-04 0:00:06 79
422 2.6687e-05 1.4021e-06 5.6292e-07 1.3137e-05 1.6019e-05 1.5646e-04 0:00:06 78
423 2.6032e-05 1.3715e-06 5.5013e-07 1.3152e-05 1.5759e-05 1.5188e-04 0:00:05 77
424 2.5294e-05 1.3295e-06 5.2225e-07 1.2987e-05 1.5594e-05 1.4733e-04 0:00:05 76
425 2.4592e-05 1.2955e-06 4.9179e-07 1.2708e-05 1.5307e-05 1.4301e-04 0:00:05 75
426 2.3932e-05 1.2627e-06 4.6507e-07 1.2395e-05 1.5009e-05 1.3876e-04 0:00:05 74
427 2.3385e-05 1.2307e-06 4.3810e-07 1.2140e-05 1.4708e-05 1.3488e-04 0:00:05 73
428 2.2702e-05 1.1964e-06 4.2895e-07 1.1815e-05 1.4400e-05 1.3073e-04 0:00:05 72
429 2.2022e-05 1.1670e-06 4.1811e-07 1.1487e-05 1.4112e-05 1.2673e-04 0:00:05 71
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
430 2.1343e-05 1.1395e-06 4.0655e-07 1.1169e-05 1.3848e-05 1.2284e-04 0:00:05 70
431 2.0688e-05 1.1132e-06 3.9297e-07 1.0890e-05 1.3585e-05 1.1911e-04 0:00:05 69
432 2.0034e-05 1.0843e-06 3.7860e-07 1.0664e-05 1.3333e-05 1.1540e-04 0:00:05 68
433 1.9420e-05 1.0540e-06 3.6509e-07 1.0486e-05 1.3077e-05 1.1182e-04 0:00:05 67
434 1.8805e-05 1.0235e-06 3.5246e-07 1.0339e-05 1.2836e-05 1.0830e-04 0:00:05 66
435 1.8237e-05 9.9361e-07 3.4089e-07 1.0207e-05 1.2613e-05 1.0488e-04 0:00:11 65
436 1.7867e-05 9.6489e-07 3.3147e-07 1.0070e-05 1.2396e-05 1.0193e-04 0:00:10 64
437 1.7249e-05 9.3696e-07 3.2369e-07 9.9127e-06 1.2178e-05 9.8453e-05 0:00:09 63
438 1.6641e-05 9.1024e-07 3.1522e-07 9.7516e-06 1.1978e-05 9.5070e-05 0:00:08 62
439 1.6075e-05 8.8445e-07 3.0657e-07 9.5558e-06 1.1782e-05 9.1782e-05 0:00:07 61
440 1.5507e-05 8.5934e-07 2.9771e-07 9.3559e-06 1.1577e-05 8.8576e-05 0:00:06 60
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
441 1.4968e-05 8.3538e-07 2.8953e-07 9.1568e-06 1.1365e-05 8.5502e-05 0:00:06 59
442 1.4435e-05 8.1092e-07 2.8200e-07 8.9150e-06 1.1117e-05 8.2511e-05 0:00:05 58
443 1.3909e-05 7.8579e-07 2.7430e-07 8.6397e-06 1.0832e-05 7.9591e-05 0:00:05 57
444 1.3412e-05 7.6158e-07 2.6646e-07 8.4626e-06 1.0593e-05 7.6697e-05 0:00:05 56
445 1.2919e-05 7.3663e-07 2.5859e-07 8.3050e-06 1.0373e-05 7.3869e-05 0:00:05 55
446 1.2427e-05 7.1352e-07 2.5085e-07 8.1582e-06 1.0160e-05 7.1115e-05 0:00:04 54
447 1.1955e-05 6.9069e-07 2.4298e-07 8.0243e-06 9.9524e-06 6.8377e-05 0:00:04 53
448 1.1489e-05 6.6829e-07 2.3505e-07 7.8889e-06 9.7458e-06 6.5707e-05 0:00:04 52
449 1.1032e-05 6.4622e-07 2.2714e-07 7.7443e-06 9.5366e-06 6.3074e-05 0:00:04 51
450 1.0579e-05 6.2457e-07 2.1937e-07 7.5954e-06 9.3280e-06 6.0527e-05 0:00:04 50
451 1.0144e-05 6.0340e-07 2.1162e-07 7.4418e-06 9.1191e-06 5.7964e-05 0:00:04 49
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
452 9.7135e-06 5.8258e-07 2.0395e-07 7.3665e-06 8.8360e-06 5.5314e-05 0:00:04 48
453 9.2886e-06 5.6204e-07 1.9649e-07 7.2087e-06 8.5800e-06 5.2727e-05 0:00:03 47
454 8.8688e-06 5.4173e-07 1.8948e-07 7.0401e-06 8.3484e-06 5.0236e-05 0:00:03 46
455 8.4674e-06 5.2178e-07 1.8271e-07 6.8741e-06 8.1313e-06 4.7804e-05 0:00:03 45
456 8.0651e-06 5.0193e-07 1.7588e-07 6.7139e-06 7.9272e-06 4.5401e-05 0:00:03 44
457 7.6692e-06 4.8215e-07 1.6868e-07 6.5103e-06 7.6893e-06 4.3049e-05 0:00:03 43
458 7.2816e-06 4.6413e-07 1.6157e-07 6.3532e-06 7.4647e-06 4.0779e-05 0:00:03 42
459 6.9007e-06 4.4677e-07 1.5472e-07 6.2169e-06 7.2585e-06 3.8520e-05 0:00:03 41
460 6.5232e-06 4.2936e-07 1.4817e-07 6.0800e-06 7.0654e-06 3.6307e-05 0:00:03 40
461 6.1553e-06 4.1215e-07 1.4195e-07 5.9460e-06 6.8798e-06 3.4156e-05 0:00:03 39
462 5.7940e-06 3.9516e-07 1.3597e-07 5.7100e-06 6.6430e-06 3.2106e-05 0:00:03 38
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
463 5.4412e-06 3.7920e-07 1.3035e-07 5.5646e-06 6.4480e-06 3.0052e-05 0:00:03 37
464 5.0931e-06 3.6342e-07 1.2498e-07 5.4463e-06 6.2742e-06 2.8058e-05 0:00:03 36
465 4.7603e-06 3.4803e-07 1.1977e-07 5.3385e-06 6.1099e-06 2.6117e-05 0:00:03 35
466 4.4465e-06 3.3302e-07 1.1462e-07 5.2286e-06 5.9490e-06 2.4227e-05 0:00:02 34
467 4.1405e-06 3.1837e-07 1.0891e-07 5.1170e-06 5.7908e-06 2.2421e-05 0:00:02 33
468 3.8459e-06 3.0411e-07 1.0351e-07 5.0083e-06 5.6444e-06 2.0604e-05 0:00:02 32
469 3.5576e-06 2.9021e-07 9.8542e-08 4.9013e-06 5.5058e-06 1.8860e-05 0:00:02 31
470 3.2977e-06 2.7672e-07 9.3865e-08 4.8026e-06 5.3697e-06 1.7171e-05 0:00:02 30
471 3.0445e-06 2.6435e-07 8.9409e-08 4.7052e-06 5.2400e-06 1.5530e-05 0:00:02 29
472 2.8185e-06 2.5267e-07 8.5100e-08 4.6136e-06 5.1154e-06 1.3972e-05 0:00:02 28
473 2.6079e-06 2.4169e-07 8.1138e-08 4.5248e-06 4.9957e-06 1.2459e-05 0:00:03 27
iter continuity x-velocity y-velocity k omega vf-vapor time/iter
474 2.4027e-06 2.3200e-07 7.7236e-08 4.4361e-06 4.8766e-06 1.1183e-05 0:00:03 26
475 2.2195e-06 2.2300e-07 7.3509e-08 4.3493e-06 4.7589e-06 9.9964e-06 0:00:03 25
! 475 solution is converged
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'file' is deprecated. Use 'settings.file' instead.
warnings.warn(
Writing to a16bfeaf8838:"/mnt/pyfluent/cav.cas.h5" in NODE0 mode and compression level 1 ...
Grouping cells for Laplace smoothing ...
3525 cells, 1 zone ...
7240 faces, 7 zones ...
3716 nodes, 1 zone ...
Done.
Done.
Writing to a16bfeaf8838:"/mnt/pyfluent/cav.dat.h5" in NODE0 mode and compression level 1 ...
Writing results.
Done.
Post Processing#
Since Fluent is being run without the GUI, we will need to export plots as picture files. Edit the picture settings to use a custom resolution so that the images are large enough.
graphics = solver.results.graphics
# use_window_resolution option not active inside containers or Ansys Lab environment
if graphics.picture.use_window_resolution.is_active():
graphics.picture.use_window_resolution = False
graphics.picture.x_resolution = 1920
graphics.picture.y_resolution = 1440
/home/ansys/actions-runner/_work/pyfluent/pyfluent/src/ansys/fluent/core/session_solver.py:309: DeprecatedSettingWarning: 'results' is deprecated. Use 'settings.results' instead.
warnings.warn(
Create contour plots#
Create a contour plot for static pressure, turbulent kinetic energy and the volume fraction of water vapor. For each plot enable banded coloring and filled option.
graphics = solver.results.graphics
graphics.contour["contour_static_pressure"] = {
"coloring": {
"option": "banded",
"smooth": False,
},
"field": "pressure",
"filled": True,
}
Note: Setting Smooth is not set as it is inactive
Mirror the display around the symmetry plane to show the full model.
solver.settings.results.graphics.views.mirror_zones = ["symm_2", "symm_1"]
graphics.contour["contour_static_pressure"].display()
graphics.picture.save_picture(file_name="contour_static_pressure.png")
Error: Values contain disallowed entries
Error Object: (symm_2 symm_1)
Creating zone surface for fluid zone
graphics.contour.create("contour_tke")
graphics.contour["contour_tke"] = {
"coloring": {
"option": "banded",
"smooth": False,
},
"field": "turb-kinetic-energy",
"filled": True,
}
graphics.contour["contour_tke"].display()
graphics.picture.save_picture(file_name="contour_tke.png")
Note: Setting Smooth is not set as it is inactive
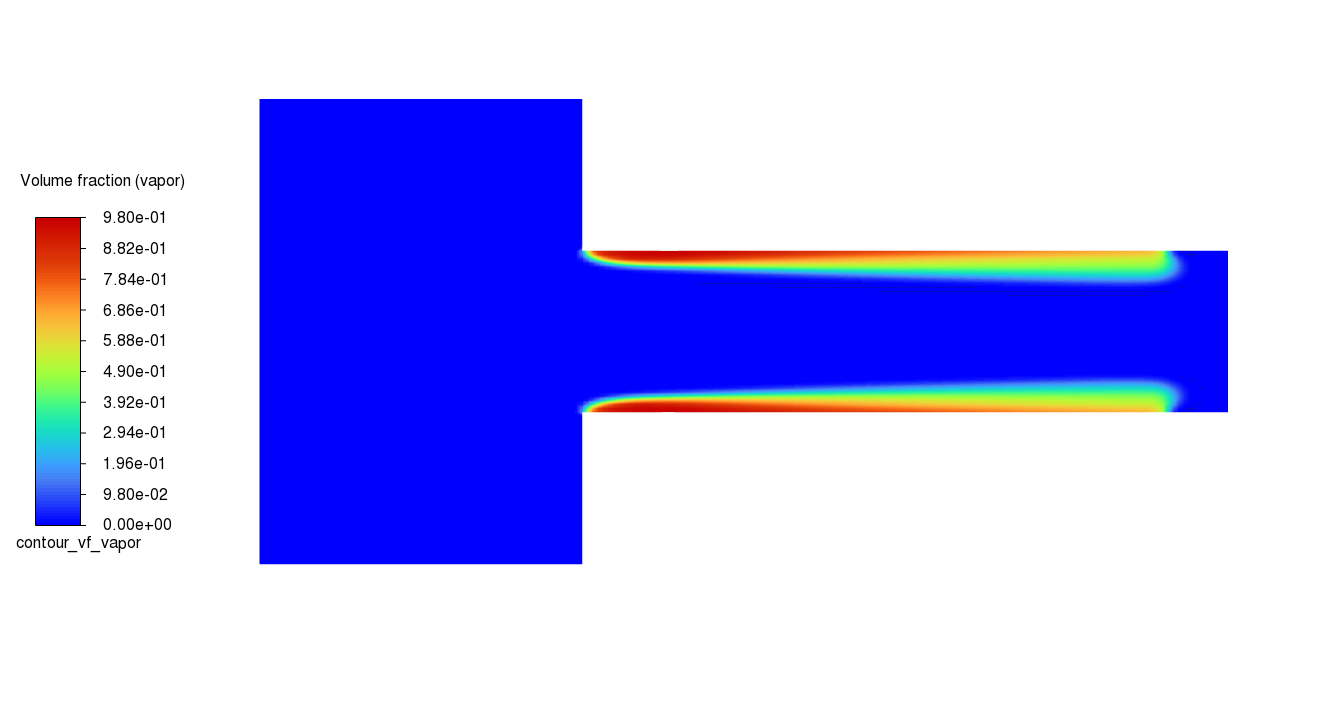
graphics.contour.create("contour_vf_vapor")
graphics.contour["contour_vf_vapor"] = {
"coloring": {
"option": "banded",
"smooth": False,
},
"field": "vapor-vof",
"filled": True,
}
graphics.contour["contour_vf_vapor"].display()
graphics.picture.save_picture(file_name="contour_vf_vapor.png")
Note: Setting Smooth is not set as it is inactive
# Save case to 'cav.cas.h5' and exit
solver.settings.file.write_case(file_name="cav.cas.h5")
solver.exit()
Writing to a16bfeaf8838:"/mnt/pyfluent/cav.cas.h5" in NODE0 mode and compression level 1 ...
Grouping cells for Laplace smoothing ...
3525 cells, 1 zone ...
7240 faces, 7 zones ...
3716 nodes, 1 zone ...
Done.
Done.
Total running time of the script: (1 minutes 48.468 seconds)